定積分の面積がマイナス?その数学的説明
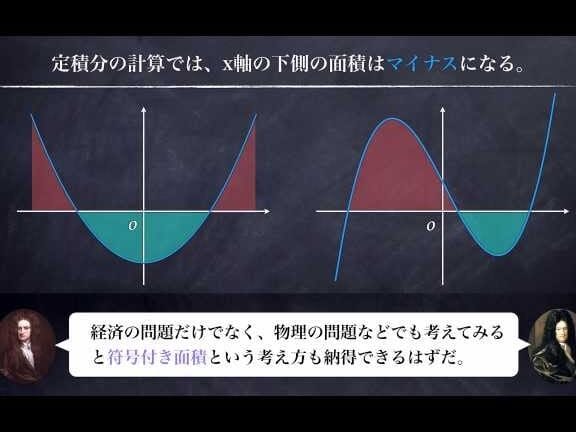
定積分の面積がマイナスという現象は、数学の世界では非常に興味深い問題となっている。積分は、面積を計算するための数学的道具であり、面積がマイナスになるということは、我々の常識を覆すものである。しかしながら、この現象を数学的に説明することができるということを知ると、数学の美しさや深さを感じることができる。本稿では、定積分の面積がマイナスになる原因を数学的に説明し、読者にこの問題に対する新しい視点を提供することを目指す。
定積分の面積がマイナス?その数学的説明
定積分の面積がマイナスになるという現象は、数学的にはどう説明するのか?この現象は、函数の積分値がマイナスになる場合、面積がマイナスになるということを意味する。このような現象は、数学的にはどう理解するのか?
函数の積分値のマイナス化
函数の積分値がマイナスになる場合、面積がマイナスになるということを意味する。このような現象は、函数の形状や積分区間によって決まり、数学的には以下の要因によって説明される:
台湾で日本語は通じる?その現状とコミュニケーション- 函数の奇関数性:函数が奇関数の場合、積分値がマイナスになる可能性がある。
- 積分区間の選択:積分区間を選択することで、積分値がマイナスになる場合がある。
- 函数のsingularity:函数にsingularityがある場合、積分値がマイナスになる可能性がある。
面積のマイナス化の意味
面積がマイナスになる場合、数学的にはどう理解するのか?このような現象は、以下の点に着目することで理解することができる:
- 函数の向き:函数の向きによって、積分値がマイナスになる場合がある。
- 積分区間の向き:積分区間の向きによって、積分値がマイナスになる場合がある。
- 幾何学的意味:幾何学的には、面積がマイナスになる場合、函数が反転していることを意味する。
数学的応用
定積分の面積がマイナスになる現象は、数学的には様々な応用がある。
- 物理学:物理学において、函数の積分値がマイナスになる場合、エネルギーがマイナスになることを意味する。
- 工学:工学において、函数の積分値がマイナスになる場合、設計の最適化において重要な要因となる。
- 計算機科学:計算機科学において、函数の積分値がマイナスになる場合、アルゴリズムの最適化において重要な要因となる。
歴史的背景
定積分の面積がマイナスになる現象は、数学史において重要な位置を占める。
ゴルゴ13のスイス銀行、その謎と実態- 古典期:古典期には、函数の積分値がマイナスになる場合、数学者たちはこの現象を理解するために努力した。
- 近代期:近代期には、函数の積分値がマイナスになる場合、数学者たちはこの現象を数学的に説明するために努力した。
- 現代期:現代期には、函数の積分値がマイナスになる場合、数学者たちはこの現象を応用するために努力した。
教育的意義
定積分の面積がマイナスになる現象は、数学教育において重要な位置を占める。
- 数学的理解:この現象を理解することで、数学的思考力を高めることができる。
- 問題解決能力:この現象を応用することで、問題解決能力を高めることができる。
- クリティカル・シンキング:この現象を分析することで、クリティカル・シンキング能力を高めることができる。
積分面積にマイナスをつけるときは?

積分面積にマイナスをつけるときは、符号のルールに従って、マイナス符号を付ける必要がある場合があります。そのルールとは、積分の範囲が原点を跨いでいる場合や、積分の値が負の値を取りうる場合などです。
積分の符号ルール
積分の符号ルールとは、積分の値にマイナス符号を付けるかどうかを決めるためのルールです。
- 積分の範囲が原点を跨いでいる場合、マイナス符号を付ける。
- 積分の値が負の値を取りうる場合、マイナス符号を付ける。
- 積分の値が正の値を取りうる場合、プラス符号を付ける。
原点を跨える積分
原点を跨える積分とは、積分の範囲が原点をまたいでいる場合です。この場合、マイナス符号を付ける必要があります。
「friends with benefits」の意味、その背景と文化- 例えば、∫(-1,1)x^2 dxのように、積分の範囲が原点を跨えている場合、マイナス符号を付ける。
- この場合、積分の値は負の値を取りうるため、マイナス符号を付ける。
負の値を取りうる積分
負の値を取りうる積分とは、積分の値が負の値を取りうる場合です。この場合、マイナス符号を付ける必要があります。
- 例えば、∫(0,π)sin(x) dxのように、積分の値が負の値を取りうる場合、マイナス符号を付ける。
- この場合、積分の値は負の値を取りうるため、マイナス符号を付ける。
積分の値の符号
積分の値の符号とは、積分の値が正の値か負の値かを示す符号です。
- 積分の値が正の値の場合、プラス符号を付ける。
- 積分の値が負の値の場合、マイナス符号を付ける。
マイナス符号の付け方
マイナス符号の付け方とは、積分の値にマイナス符号を付ける方法です。
金にならない仕事、その魅力とやりがい- 積分の値の前にマイナス符号を付ける。
- 例えば、-∫(0,1)x^2 dxのように、マイナス符号を付ける。
定積分の公式は?
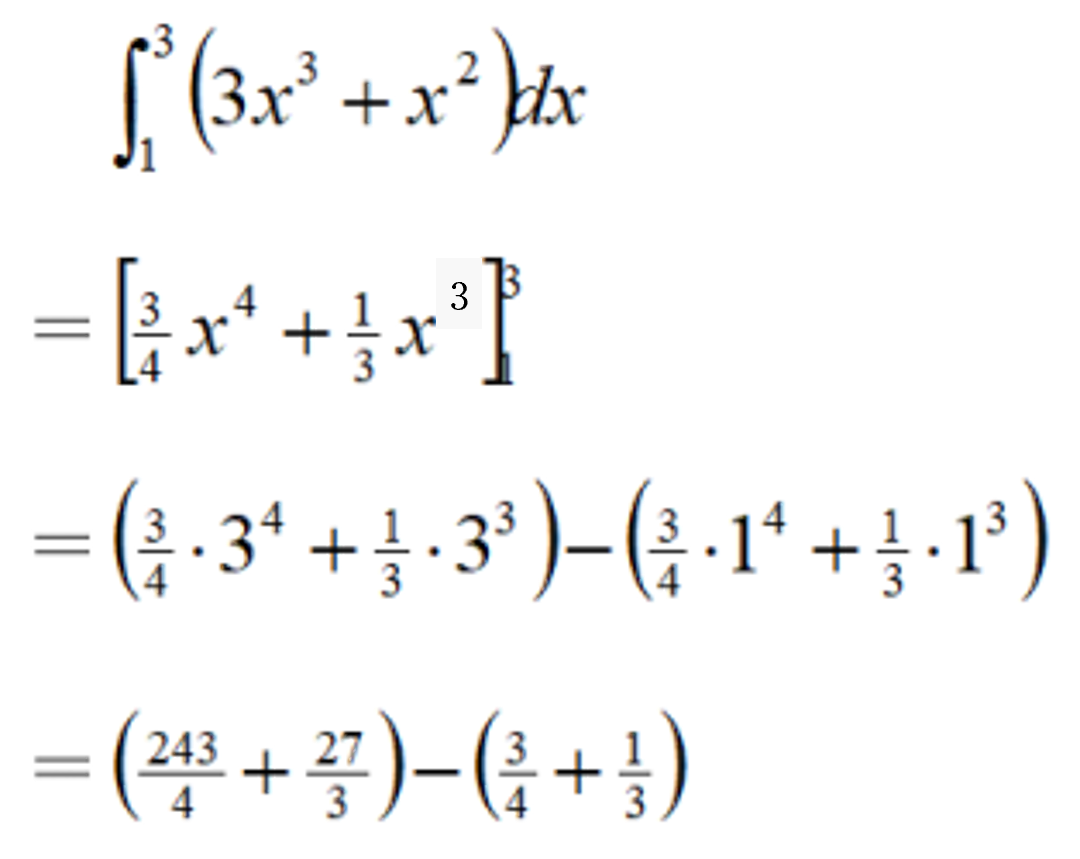
定積分の公式は、Newton-Leibnizの公式(ニュートン・ライプニッツの公式)と呼ばれるもので、以下の式で表される。
∫[a, b] f(x) dx = F(b) – F(a)
アムウェイの何が悪い?その問題点と対策ここで、f(x) は積分函数、F(x) はその反導函数、a と b は積分区間の境界値である。
Newton-Leibnizの公式の証明
Newton-Leibnizの公式の証明は、微分積分学(みぶんせきがく)の基礎的な定理を用いて行う。まず、函数 f(x) の反導函数 F(x) を考える。次に、区間 [a, b] 上での積分 ∫[a, b] f(x) dx を、リーマン和(りーわんわ)を用いて近似する。最後に、リーマン和の限界をとって、Newton-Leibnizの公式を導出する。
Newton-Leibnizの公式の応用
Newton-Leibnizの公式は、積分の計算(せきぶんのけいさん)や微分方程式(みぶんほうていしき)の解法に広く応用される。例えば、以下のような問題に適用できる。
- 積分 ∫[0, 1] x^2 dx の計算
- 微分方程式 dy/dx = x^2 の解法
- 曲線の面積や体積の計算
Newton-Leibnizの公式の歴史
Newton-Leibnizの公式は、アイザック・ニュートン(アイザック・ニュートン)とゴットフリート・ヴィルヘルム・ライプニッツ(ゴットフリート・ヴィルヘルム・ライプニッツ)によって独立に発見された。ニュートンは1665年に、この公式を用いて無限級数(むげんきゅうすう)を研究した。ライプニッツは1676年に、この公式を用いて微分積分学(みぶんせきがく)を体系化した。
Newton-Leibnizの公式の一般化
Newton-Leibnizの公式は、線積分(せんせきぶん)や曲面積分(きょくめんせきぶん)にも一般化される。線積分では、ベクトル解析(べくとるかいせき)を用いて、曲線上での積分を計算する。曲面積分では、微分幾何学(みぶんきかがく)を用いて、曲面上での積分を計算する。
Newton-Leibnizの公式の相關字段
Newton-Leibnizの公式は、微分積分学(みぶんせきがく)や数学物理学(すうがくぶつりがく)などの分野と深く関係している。微分積分学では、微分方程式(みぶんほうていしき)や積分方程式(せきぶんほうていしき)を研究する。数学物理学では、力学系(りょくがくけい)や電磁気学(でんじきがく)などの分野で、Newton-Leibnizの公式を応用する。
放物線と接線の面積を求める公式は?
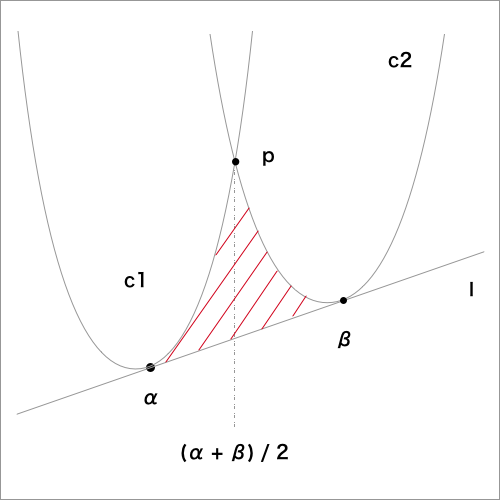
放物線と接線の面積を求める公式は、ガウス・ボネの公式を用いることで計算することができます。この公式は、放物線の曲率半径、接線の長さ、 그리고放物線と接線が交わる点の座標を用いて、面積を計算することができます。
ガウス・ボネの公式の導出
ガウス・ボネの公式は、数学者ガウスとボネが導出した公式です。この公式は、放物線の曲率半径と接線の長さを用いて、面積を計算することができます。導出の過程では、微積分学の知識が必要です。
放物線の曲率半径の計算
放物線の曲率半径は、放物線の式から計算することができます。具体的には、放物線の式を微分し、放物線の接線の式を計算し、曲率半径を計算することができます。
- 放物線の式を微分し、傾きを計算する
- 傾きから曲率半径を計算する
- 曲率半径を用いてガウス・ボネの公式に代入する
接線の長さの計算
接線の長さは、放物線と接線が交わる点の座標から計算することができます。具体的には、放物線の式と接線の式を用いて、交点の座標を計算し、接線の長さを計算することができます。
- 放物線の式と接線の式を用いて、交点の座標を計算する
- 交点の座標から接線の長さを計算する
ガウス・ボネの公式の応用
ガウス・ボネの公式は、放物線と接線の面積を計算する以外にも、様々な応用があります。例えば、曲線の長さ、曲面の面積の計算などに用いることができます。
- 曲線の長さの計算
- 曲面の面積の計算
- その他の応用
計算の注意点
ガウス・ボネの公式を用いて面積を計算する際には、注意点があります。例えば、放物線の曲率半径や接線の長さの計算には、微積分学の知識が必要です。また、計算の過程では、計算ミスに注意する必要があります。
- 微積分学の知識を用いて計算する
- 計算ミスに注意する
定積分の上端と下端は入れ替えられますか?

定積分の上端と下端は入れ替えられません。なぜなら、積分の定義によって、上端と下端が入れ替えられることは許されていないからです。積分の定義によると、積分の値は上端から下端に向かって計算されるため、上端と下端を入れ替えると積分の値が変わってしまうためです。
積分の性質
積分は、線形性を持つという性質があります。この性質により、積分の値は積分の上端と下端の値との差に依存します。上端と下端を入れ替えると、積分の値が変化することになります。
- 積分の線形性
- 積分の値の計算
- 上端と下端の入れ替えの影響
積分の種類
積分には、定積分と不定積分の2種類があります。定積分は、上端と下端が決まっている積分であり、不定積分は、上端と下端が決まっていない積分です。不定積分では、上端と下端を入れ替えることができますが、定積分では入れ替えることができません。
- 定積分
- 不定積分
- 両者の違い
積分の応用
積分は、数学や物理学などの分野で広く応用されています。積分は、面積や体積の計算、運動の描写、電気回路の分析などに使用されます。積分の応用において、上端と下端を入れ替えることは、計算結果に影響を与えるため避ける必要があります。
- 数学での応用
- 物理学での応用
- 電気回路の分析
積分の誤り
積分において、上端と下端を入れ替えることは、計算結果に誤りを生じます。特に、物理的意味を持つ積分においては、上端と下端を入れ替えることは、物理的現象を正しく捉えることができません。
- 物理的意味
- 計算結果の誤り
- 物理的現象の捉え方
積分の歴史
積分の歴史において、古代ギリシアでは、積分の概念が既に存在していました。ただし、積分の公式化は、17世紀以降に行われました。当時の数学者たちは、積分の上端と下端を入れ替えることを許されていなかったため、積分の値の計算に注意を払う必要がありました。
- 古代ギリシアにおける積分
- 17世紀以降の積分の公式化
- 数学者の注意
詳しくは
定積分の面積がマイナスになる理由は何ですか?
定積分の面積がマイナスになる理由は、積分の方向と関数の符号によって決まります。積分の方向が正しい方向に向いている場合、積分の結果は正の値を示します。一方、積分の方向が逆方向に向いている場合、積分の結果は負の値を示します。つまり、積分の方向が逆転すると、積分の結果も逆転します。このため、定積分の面積がマイナスになる場合があるのです。
また、積分する関数の符号も重要です。積分する関数が正の値を示す場合、積分の結果も正の値を示します。一方、積分する関数が負の値を示す場合、積分の結果も負の値を示します。したがって、積分する関数の符号も、定積分の面積がマイナスになる理由の一つです。
マイナスの面積は何を意味しますか?
マイナスの面積は、向きを反対にした積分の結果を示します。つまり、マイナスの面積は、積分する関数が反対方向に伸びていることを意味します。
例えば、ある関数が正の値を示す場合、その関数の積分結果も正の値を示します。しかし、その関数に反対方向の向きを持つ関数を積分すると、マイナスの面積を示すことになります。このため、マイナスの面積は、積分する関数の向きを反対にすることを意味します。
マイナスの面積を計算するには、どうすればよいですか?
マイナスの面積を計算するには、積分する関数の符号を変える必要があります。積分の方向を逆転するか、積分する関数の符号を反転することで、マイナスの面積を計算することができます。
例えば、ある関数の積分結果がマイナスである場合、積分する関数の符号を反転することで、積分結果を正の値に変えることができます。同様に、積分の方向を逆転することで、マイナスの面積を計算することができます。
マイナスの面積が現れる状況はどこですか?
マイナスの面積が現れる状況は、物理現象や実験データなど、様々な分野で現れます。
例えば、力学の分野では、力の向きが逆転する場合、積分結果がマイナスになる場合があります。また、電気工学の分野では、電流の向きが逆転する場合、積分結果がマイナスになる場合があります。これらの場合、マイナスの面積が現れる状況が生じます。