行列基底の求め方、その数学的解説

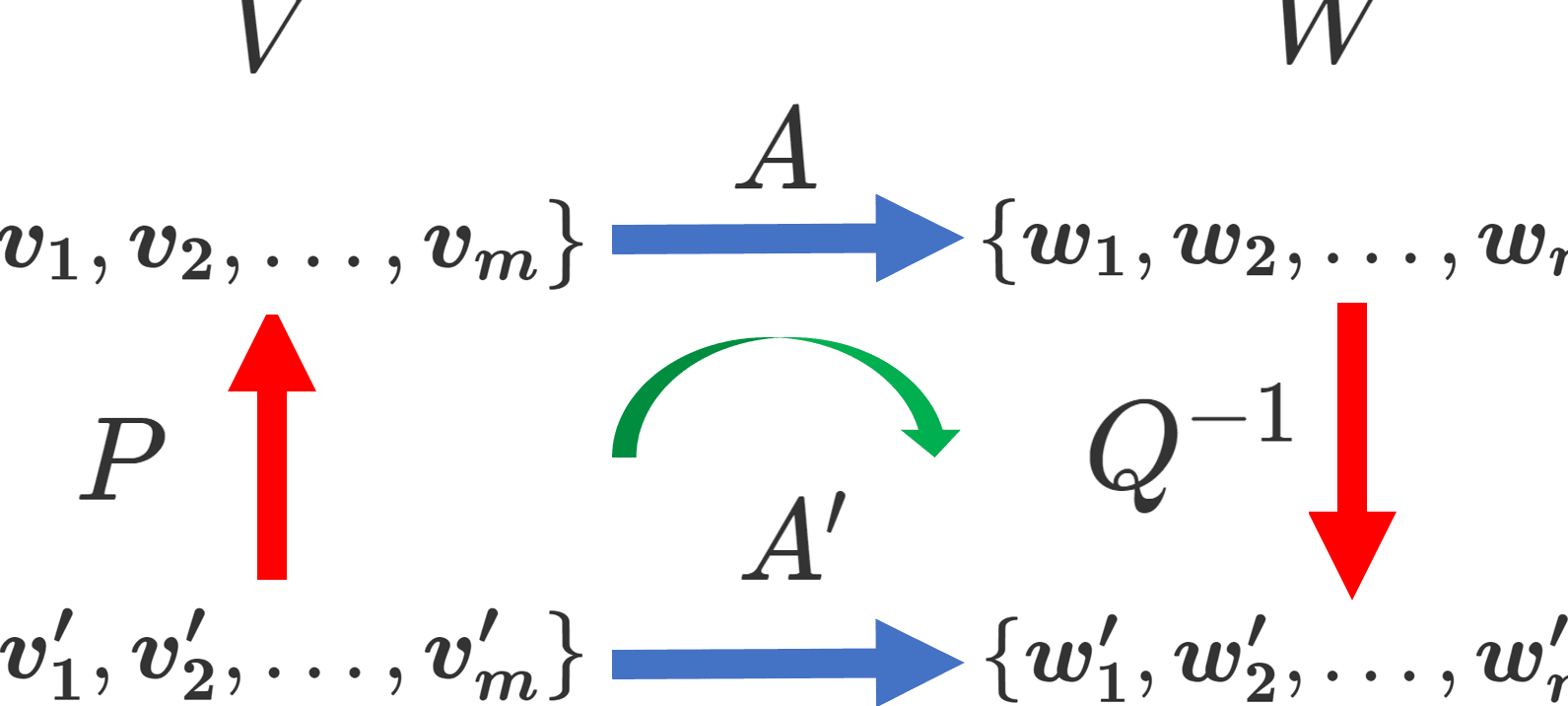
数理の世界では、ベクトルの概念が中心的な役割を果たす。特に、行列基底の存在は、線形代数の理論を支える柱の一つである。行列基底とは、あるベクトル空間における基底ベクトルの集合のことで、 線形独立なベクトルたちからなる。ここでは、行列基底の求め方について、数学的な解説を行う。具体的には、基底変換行列の計算方法や、基底の正規直交化について説明する。

行列基底の求め方、その数学的解説

行列基底（Matrix Basis）とは、行列の基底ベクトルを求めるための方法であり、線形代数の基礎的概念の一つです。以下では、行列基底の求め方について詳細に説明します。

行列の基底とは

行列の基底とは、行列の列ベクトルがspanする空間の基底ベクトルを指します。行列A(m×n)の基底ベクトルは、Aの列ベクトルが生成する空間の基底ベクトルであり、Aのrankの数だけ存在します。基底ベクトルは、線形独立であることが必要です。

教師と生徒が結婚、その合法性と倫理

行列基底の求め方

行列基底の求め方には、ガウスの消去法や、列 echelon 形、QR 分解などがあります。ガウスの消去法では、行列Aを上三角行列に変換し、階数を計算します。列 echelon 形では、行列Aを列 echelon 形に変換し、基底ベクトルを計算します。QR 分解では、行列AをOrthogonal 行列Qと上三角行列Rに分解し、基底ベクトルを計算します。

数学的解説

数学的には、行列基底は、行列の列ベクトルがspanする空間の基底ベクトルを指します。行列A(m×n)の基底ベクトルは、Aの列ベクトルが生成する空間の基底ベクトルであり、Aのrankの数だけ存在します。基底ベクトルは、線形独立であることが必要です。

応用例

行列基底の応用例として、線形回帰分析や、主成分分析、クラスター分析などがあります。線形回帰分析では、行列基底を用いて、最適な回帰係数を計算します。主成分分析では、行列基底を用いて、データの次元削減を行います。クラスター分析では、行列基底を用いて、データのクラスターを生成します。

磁石にくっつく金属、その種類と用途

計算例

計算例として、以下のような例を考えてみます。

1. 行列A = [[1, 2], [3, 4]]の基底ベクトルを計算する。
2. 行列A = [[1, 1], [1, 2]]の基底ベクトルを計算する。
3. 行列A = [[1, 2, 3], [4, 5, 6]]の基底ベクトルを計算する。

以上のように、行列基底の求め方について説明しました。

常温核融合技術、その可能性とトヨタの取り組み

基底行列とは何ですか？

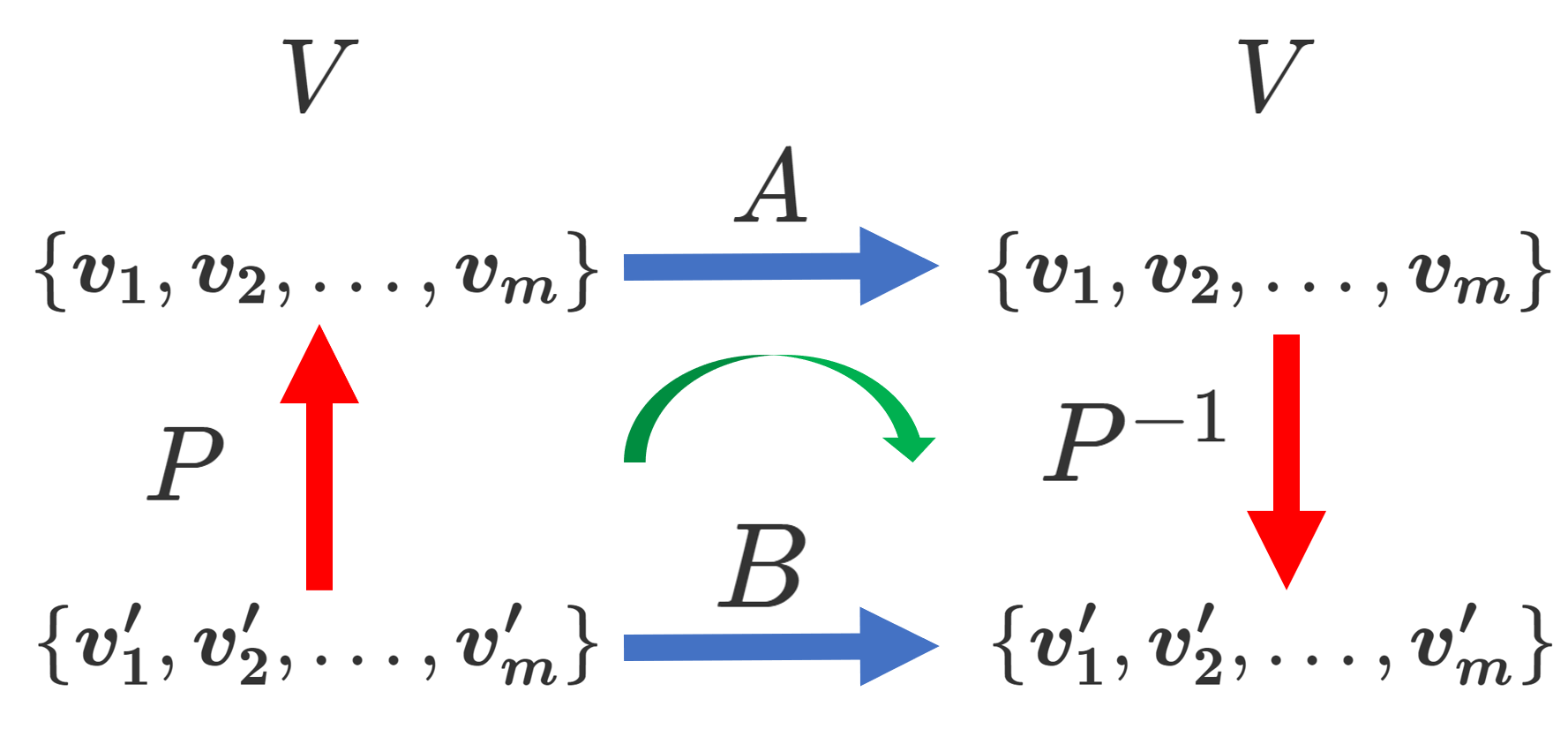
基底行列とは、線型代数において、ベクトル空間の上に定義される行列のことを指します。基底とは、ベクトル空間を生成するために必要な最小のベクトルの集合であり、行列とは、ベクトルを並べた表形式を指します。基底行列は、ベクトル空間の基底を並べた表形式であり、線型変換を表現するために使用されます。

基底行列の性質

基底行列は、以下の性質を持っています。

銅と濃硝酸、その化学反応と実験

1. 基底行列は、正方行列である。
2. 基底行列の行列式は、0以外である。
3. 基底行列は、逆行列を持つ。

基底行列の種類

基底行列には、以下の種類があります。

1. 標準基底行列：標準基底ベクトルで構成される基底行列。
2. 直交基底行列：直交基底ベクトルで構成される基底行列。
3. 正規直交基底行列：正規直交基底ベクトルで構成される基底行列。

基底行列の応用

基底行列は、以下の分野で応用されます。

1. 線型代数：線型変換の表現などに使用されます。
2. 機械学習：特徴量の抽出や次元削減などに使用されます。
3. 信号処理：信号の変換やフィルタリングなどに使用されます。

基底行列の計算方法

基底行列の計算には、以下の方法があります。

キスマイフット2の意味、その由来とファンの声

1. ガウスの消去法：ガウスの消去法を用いて基底行列を計算します。
2. QR分解：QR分解を用いて基底行列を計算します。
3. 固有値分解：固有値分解を用いて基底行列を計算します。

基底行列の注意点

基底行列には、以下の注意点があります。

1. 基底行列は、非invertibleになる場合がある。
2. 基底行列は、計算コストが高くなる場合がある。
3. 基底行列は、数値的不安定になる場合がある。

線形代数でKとは何ですか？

線形代数でKとは、何ですか？

スタバのコールドブリューがまずい、その理由と他の選択肢

Kは、線形代数の分野でよく使われる記号です。体(field)や環(ring)を表すために使用されます。特に、体K上のベクトル空間や、K環上の加群の理論において重要な役割を果たします。

体Kとその性質

体Kは、加法と乗法の二つの演算を持つ代数的構造体です。交換律や結合律、分配律などの性質を満たすことが求められます。これらの性質によって、体K上での演算がうまく定義されるようになります。

1. 交換律：a + b = b + a、a × b = b × a
2. 結合律：(a + b) + c = a + (b + c)、(a × b) × c = a × (b × c)
3. 分配律：a × (b + c) = a × b + a × c

K環とその性質

K環は、体K上で定義される環構造体です。加法単位元0と乗法単位元1を持ちます。

1. 加法単位元：a + 0 = a
2. 乗法単位元：a × 1 = a

K環においては、可換環や整域などの性質が成り立つ場合があります。

K上のベクトル空間

K上のベクトル空間は、体K上で定義されるベクトル空間です。スカラー倍やベクトルの加法の演算が定義されます。

1. スカラー倍：ka、k ∈ K、a ∈ V
2. ベクトルの加法：a + b、a, b ∈ V

K環上の加群

K環上の加群は、K環上で定義される加群構造体です。スカラー倍や加法の演算が定義されます。

1. スカラー倍：ka、k ∈ K、a ∈ M
2. 加法：a + b、a, b ∈ M

線形代数の応用

線形代数の理論は、物理学、工学、コンピューター科学など多くの分野で応用されます。行列理論やベクトル解析などの技術を通じて、実際の問題を解くことができます。

1. 画像処理：行列を用いた画像変換や、ベクトルを用いた画像検出
2. 機械学習：行列を用いた機械学習のアルゴリズム
3. 物理工学：ベクトルを用いた運動方程式の解析

基底と次元の違いは何ですか？

基底と次元は、数学や物理学において重要な概念ですが、しばしば混同されます。基底は、ベクトル空間において、線形独立なベクトルの集合であり、次元は、ベクトル空間の個数を表します。例えば、2次元空間では、基底は2つの線形独立なベクトルで構成されます。

基底の定義

基底は、ベクトル空間において、線形独立なベクトルの集合であり、全てのベクトルを表すことができます。

1. 線形独立：基底ベクトル同士が線形独立であることを示します。
2. 生成集合：基底ベクトルを線形結合した結果、全てのベクトルを生成することができます。
3. 最小生成集合：基底ベクトルが最小の集合であることを示します。

次元の定義

次元は、ベクトル空間の個数を表します。

1. スカラー倍：ベクトル空間のスカラー倍によって、次元が変化します。
2. 線形独立：次元は、線形独立なベクトルの個数に相当します。
3. ベクトル空間の構成：次元は、ベクトル空間を構成する要素の個数に相当します。

基底と次元の関係

基底と次元は、紧密な関係にあります。

1. 基底の個数が次元に等しい：基底の個数は、次元に等しくなります。
2. 次元の変化：基底の個数が変化すると、次元も変化します。
3. 基底の変更：基底を変更すると、次元も変更される可能性があります。

基底の例

基底の例として、2次元空間の基底を挙げます。

1. i = (1, 0)：x軸方向の単位ベクトル
2. j = (0, 1)：y軸方向の単位ベクトル

この2つの基底ベクトルを線形結合することで、2次元空間の全てのベクトルを生成することができます。

次元の例

次元の例として、3次元空間の次元を挙げます。

1. x軸方向の次元
2. y軸方向の次元
3. z軸方向の次元

この3つの次元を併せると、3次元空間を構成することができます。

数学における行列の定義は？

数学における行列の定義は、数値や式を並べた表形式のデータ構造体です。行列は、数学や物理学、工学などの分野で広く用いられており、様々な問題を解くために使用されます。

行列の種類

行列には、様々な種類があります。

1. 零行列：全ての要素が0である行列
2. 単位行列：対角線上の要素が1で、他は0である行列
3. 対角行列：対角線上の要素が非ゼロで、他は0である行列

行列の操作

行列には、加算、減算、乗算、除算などの操作があります。

1. 行列の加算：同じ大きさの行列同士を足し合わせる
2. 行列の乗算：行列同士を掛け合わせる
3. 行列の逆数：行列の乗算に対応する操作

行列の応用

行列は、様々な分野で応用されています。

1. 線形代数：方程式の解き方や、ベクトルの計算に用いる
2. 物理学：運動方程式の解き方や、力学系の分析に用いる
3. 機械学習：データの分析や、予測モデルの構築に用いる

行列の表現

行列は、様々な方法で表現されます。

1. 行列表現：行列を表形式で表す
2. ベクトル表現：行列をベクトルの列として表す
3. 数値表現：行列を数値として表す

行列の計算

行列の計算には、多くのアルゴリズムや手法が存在します。

1. ガウスの消去法：行列の逆数を計算するためのアルゴリズム
2. LU分解：行列を下三角行列、上三角行列に分解する
3. Cholesky分解：対称行列を下三角行列に分解する

詳しくは

行列基底を求めるための必要条件とは何ですか?

行列基底を求めるためには、まずその行列が正則行列である必要があります。正則行列とは、逆行列が存在する行列のことを指します。逆行列が存在するためには、行列の秩が最大値である必要があります。秩が最大値であるとは、行列の列ベクトルが線形独立であることを意味します。線形独立であるとは、各列ベクトルが他antzの列ベクトルの線形結合によって表されないことを意味します。

行列基底の求め方は何ですか?

行列基底を求めるためには、ガウスの消去法や LU分解などの方法があります。ガウスの消去法とは、行列を上三角行列に変換することで、基底を求める方法です。LU分解とは、行列を下三角行列と上三角行列に分解することで、基底を求める方法です。これらの方法で、行列の基底を求めることができます。

行列基底の数学的解説とは何ですか?

行列基底の数学的解説とは、線形代数における概念です。線形代数では、行列を用いて、ベクトル空間上での線形写像を表現します。行列基底とは、ベクトル空間上での基底を、行列の形で表現したものです。行列基底を求めることで、ベクトル空間上での基底を明確化することができます。

行列基底を求めることで何が利便ですか?

行列基底を求めることで、線形変換や固有値の計算ができます。線形変換とは、ベクトル空間上での線形写像のことを指します。固有値とは、線形変換がもつスカラー値のことを指します。行列基底を求めることで、線形変換や固有値の計算が簡単になります。また、最小二乗法や主成分分析などの統計的解析でも、行列基底を求めることが必要になります。