d2x/dt2、その数式が示すもの

微分方程式における2階導関数が表す物理的意味について考えてみましょう。

d²x/dt² が示すもの

d²x/dt² の意味

d²x/dt² は、物理学や数学において、変位 x の時間 t に対する 2 階微分を表す式です。

d²x/dt² が表す物理量

d²x/dt² は、加速度を表します。つまり、ある物体の速度が時間とともにどれだけ変化するかを示す量です。

寿命がない生き物、その不思議な存在とメカニズム

加速度の意味

加速度とは、速度の変化率です。速度が一定の速さで増加している場合、加速度は一定の値となります。速度が変化していない場合は、加速度は 0 となります。

加速度の単位

加速度の単位は、メートル毎秒毎秒 (m/s²) です。

d²x/dt² の応用

d²x/dt² は、運動学や力学など、様々な分野で用いられます。例えば、物体の運動を記述したり、物体に働く力を計算したりするために使われます。

マッハ20の戦闘機、その驚異のスピードと性能

d²x/dt² の例

d²x/dt² が表す加速度の例をいくつか挙げます。

1. 重力加速度: 地球上の物体が落下する際に感じる加速度で、約 9.8 m/s² です。
2. 自動車の加速度: 自動車が加速する際に感じる加速度です。自動車の性能によって異なりますが、一般的に 0～5 m/s² 程度の加速度です。
3. ロケットの加速度: ロケットが打ち上げられる際に感じる加速度です。非常に大きな加速度で、数百 m/s² に達することもあります。

数学でDは何を表しますか？

数学におけるDの表記

数学では、”D”は様々な意味を持ち、文脈によって解釈が変わります。いくつかの一般的な意味を以下に示します。

検索エンジンが日本製、その背景と可能性

導関数

微分積分学において、”D”は導関数を表す記号としてよく用いられます。例えば、関数f(x)の導関数は、D(f(x))またはDf(x)と表記されます。

行列式

線形代数学において、”D”は正方行列の行列式を表す記号として用いられます。行列式は、行列の重要な性質であり、線形変換の拡大率や逆行列の存在判定などに用いられます。

差分

差分方程式や差分法において、”D”は差分演算子を表す記号として用いられます。差分演算子は、ある値とその一つ前の値の差を求める演算子であり、離散的なデータの解析に用いられます。

SSDとSDカードの違い、その選び方と用途

次元

幾何学やベクトル空間において、”D”は次元を表す記号として用いられます。例えば、三次元空間はD=3と表記されます。

データ

統計学やデータ分析において、”D”はデータセットを表す記号として用いられることもあります。特に、データセット内の特定の変数を表すために用いられます。例えば、D1はデータセット内の最初の変数を表すことができます。

Dy/dx D の意味は？

高知能者の特徴、その脳と日常生活

Dy/dx D の意味

Dy/dx D は、微分方程式における微分演算子を表す記号です。これは、微分方程式の解を求める際に、解の導関数を求める操作を簡潔に表現するために用いられます。

微分演算子の役割

微分演算子は、関数に対して微分という操作を行うものであり、関数とその導関数の関係を表します。微分方程式は、未知の関数とその導関数の関係式で表され、微分演算子はこの関係式を簡潔に表現するために用いられます。

Dy/dx D の具体的な例

例えば、y” + 2y’ + y = 0 という微分方程式の場合、微分演算子 D を用いて次のように表すことができます。

電線と光ケーブルの見分け方、そのポイントと実例

1. y” を D²y と表す。
2. y’ を Dy と表す。
3. 微分方程式を (D² + 2D + 1)y = 0 と表す。

微分演算子の利点

微分演算子を用いることで、微分方程式を代数的な式として扱うことができ、解を求めるための計算が簡略化されます。また、微分方程式の解の構造を理解する上でも役立ちます。

微分演算子の応用

微分演算子は、数学、物理学、工学など様々な分野で応用されています。例えば、熱伝導方程式や波動方程式などの偏微分方程式の解を求める際に用いられます。また、信号処理や制御理論などでも重要な役割を果たしています。

DYDXとはどういう意味ですか？

DYDXとは何か？

DYDXは、分散型取引所（DEX）の名称です。従来の中央集権型取引所とは異なり、DYDXはブロックチェーン技術に基づいて構築されており、第三者の仲介者を介さずにユーザー同士が直接取引を行うことができます。

DYDXの仕組み

DYDXは、Ethereumのブロックチェーン上で動作する分散型アプリケーション（dApp）です。ユーザーは、DYDXプラットフォームに資金を預け入れ、それを利用して他のユーザーと取引を行うことができます。取引は、スマートコントラクトによって自動的に実行され、透明性と信頼性を確保しています。

DYDXの特徴

DYDXは、以下のような特徴を持つ分散型取引所です。

1. 高速な取引実行：DYDXは、他のDEXと比べて高速な取引処理を実現しています。
2. 低い取引手数料：従来の中央集権型取引所と比べて、取引手数料が低くなっています。
3. 高い流動性：DYDXは、多くの取引ペアと高い流動性を提供しています。
4. セキュリティの向上：ブロックチェーン技術に基づいているため、セキュリティ面においても高い水準を誇ります。

DYDXの利用方法

DYDXを使用するには、まず、DYDXプラットフォームにアカウントを作成する必要があります。アカウントを作成したら、資金を預け入れ、取引を開始することができます。

DYDXの将来性

DYDXは、分散型金融（DeFi）の成長に伴い、ますます注目を集めています。将来的には、DYDXは、従来の中央集権型取引所を凌駕する存在になる可能性を秘めています。

微分方程式は何を表す？

微分方程式とは何か

微分方程式は、未知の関数とその導関数の関係を表す数学的な方程式です。簡単に言えば、ある関数の変化率を記述する方程式です。

微分方程式の表現

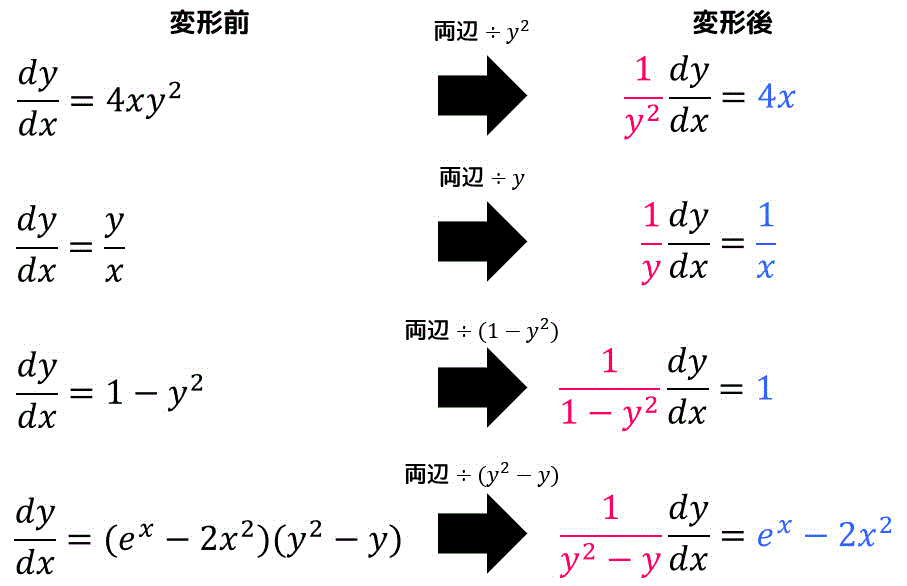
微分方程式は、未知の関数とその導関数を含む式で表現されます。たとえば、$y = f(x)$ を未知の関数とすると、微分方程式は次のように表すことができます。

dy/dx + 2y = 0

この式は、$y$ の導関数 $dy/dx$ が、$y$ の2倍に等しいことを示しています。

微分方程式の種類

微分方程式は、次数や線形性などの様々な特性に基づいて分類されます。

次数は、微分方程式に含まれる最高位の導関数の次数です。
線形性は、未知の関数とその導関数が線形に含まれているかどうかで決まります。

微分方程式の応用

微分方程式は、物理学、化学、生物学、経済学など、様々な分野で幅広く応用されています。

物理学では、運動方程式や熱伝導方程式などの記述に利用されます。
化学では、化学反応速度論や反応拡散方程式などの記述に利用されます。
生物学では、個体群動態モデルや神経系モデルなどの記述に利用されます。
経済学では、経済成長モデルや金融市場モデルなどの記述に利用されます。

微分方程式の解法

微分方程式を解くことは、与えられた条件を満たす関数を求めることになります。解法は、方程式の種類や条件によって異なります。

変数分離法
積分因子法
ラプラス変換法
数値解法

微分方程式を解くことで、物理現象や社会現象などの様々な現象を理解することができます。

詳しくは

d2x/dt2、その数式が示すものは何ですか？

d2x/dt2は、変数xの、時間tに関する2階微分を表す数式です。簡単に言えば、これは変数xの加速度を表しています。

例えば、ある物体の位置が時間tの関数x(t)で表されるとします。このとき、d2x/dt2は、その物体の時間tにおける加速度を表します。言い換えれば、d2x/dt2は、その物体の速度の時間変化率を表すのです。

なぜd2x/dt2は加速度を表すのですか？

d2x/dt2は、xの時間変化率の時間変化率を表しています。言い換えれば、これは速度の時間変化率を表しています。速度の時間変化率は、加速度の定義そのものです。

例えば、ある物体が一定の速度で移動している場合、その速度は変化せず、加速度はゼロになります。一方、物体が加速している場合、その速度は時間とともに変化し、加速度はゼロではありません。d2x/dt2は、この速度の変化を測定する式なのです。

d2x/dt2はどのような分野で用いられますか？

d2x/dt2は、物理学、工学、数学など、様々な分野で用いられます。例えば、物理学では、物体の運動を記述するために、d2x/dt2が用いられます。工学では、機械の動きや振動を解析するために、d2x/dt2が用いられます。数学では、微分方程式を解くために、d2x/dt2が用いられます。

d2x/dt2は、非常に重要な数学的概念であり、様々な分野で応用されています。

d2x/dt2の具体的な例を教えてください。

例えば、自由落下する物体の運動を考えましょう。物体の位置をx(t)とすると、その加速度は重力加速度gであり、d2x/dt2 = -gとなります。つまり、物体の加速度は常に一定であり、重力加速度と反対方向となります。

このように、d2x/dt2は、物体の運動を記述するために用いられます。