0は自然数か?数学の深淵に迫る驚きの真実

数学の偉大な謎のひとつに、「0は自然数か?」という問いがあります。この素朴な質問は、数学の根源的な定義に深く切り込むもので、長年にわたって数学者たちを悩ませてきました。
0は自然数?数学の深淵に迫る驚きの真実
0は自然数か?数学の深淵に迫る驚きの真実
1. 自然数の定義:歴史と多様性
自然数は、人間の最も基本的な数学的概念の一つです。しかし、その定義は、時代や文化によって異なります。
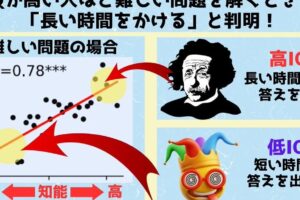
IQが低い人の顔、その共通点と特徴に迫る 古代ギリシャ: 自然数は、1から始まる正の整数と定義されていました。
現代数学: 自然数は、0を含めて1から始まる正の整数と定義されることが多いですが、0を含まない定義を採用する数学者もいます。
2. 0の特殊性:存在と役割
0は、数として特別です。それは、数の始まりであり、加算と減算の単位元であり、乗算の零元でもあります。
0は、何もないことを表す一方で、位置値記数法において重要な役割を果たしています。
0の存在は、数の概念を大きく拡張し、数学の発展に貢献しました。
3. 0は自然数か?数学界の議論
0が自然数に含まれるかどうかは、数学界で長年議論されてきました。
0を含む定義では、自然数は連続的な集合となり、数学的な操作がよりスムーズになります。
0を含まない定義では、自然数は離散的な集合となり、特に組合せ論や数論において優位性があります。
4. 0の自然数への包含:メリットとデメリット
0を自然数に含めることは、利点と欠点の両方があります。
寿命の短い生き物、その驚きの真実と背景 メリット: 自然数の集合が統一され、数学的な操作が簡素化されます。
デメリット: 伝統的な自然数の定義との矛盾が生じ、一部の数学的議論では混乱を招く可能性があります。
5. 結論:数学の深淵に迫る
0は自然数か?その答えは、数学的な定義や考え方によって異なります。重要なのは、0の役割と存在を理解し、数学の深淵を探求することです。
0を自然数に含めるのはなぜですか?
0を自然数に含める理由
0を自然数に含めるかどうかは、数学の分野によって異なります。現代の数学では、0を自然数に含めることが多いですが、歴史的には0を自然数に含まないという考え方が主流でした。この違いは、自然数の定義の解釈の違いによるものです。
歴史的な理由
歴史的には、自然数は「数えるための数」として定義されていました。つまり、物体を数える際に使用する数です。0は何もない状態を表すため、数えるための数には含まれませんでした。そのため、古代ギリシャの数学者や中世の数学者は、0を自然数に含めませんでした。
現代数学における定義
現代数学では、自然数は、「ゼロを含む正の整数」と定義されることが多いです。この定義では、0は自然数に含まれます。これは、0が数学における様々な演算において重要な役割を果たすためです。
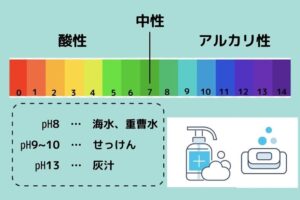
塩基性とアルカリ性の違い、その基礎知識を徹底解説0の数学的な役割
- 加算の単位元: 0は加算の単位元です。つまり、任意の自然数nに対して、n + 0 = nが成り立ちます。
- 減算の単位元: 0は減算の単位元でもあります。つまり、任意の自然数nに対して、n – 0 = nが成り立ちます。
- 乗算の零元: 0は乗算の零元です。つまり、任意の自然数nに対して、n × 0 = 0が成り立ちます。
0を含むことの利便性
0を自然数に含めることで、数学の理論や計算がよりシンプルになります。例えば、自然数の集合を{1, 2, 3, …}と定義するよりも、{0, 1, 2, 3, …}と定義する方が、数学的な表現や議論が簡潔になります。また、0を自然数に含めることで、様々な数学的な定理や公式がより一般化され、適用範囲が広がります。
0以上の整数をどう言い換えますか?

0以上の整数を言い換える方法はいくつかあります。状況や表現したいニュアンスによって適切な言い換えが異なります。以下に、いくつかの言い換えとその説明を挙げます。
死ぬ前の匂い、その科学的説明と実話に迫る自然数
0を含まない正の整数を「自然数」と呼びます。自然数は、1, 2, 3, 4, 5…のように、自然界で数える際に用いられる数です。 0は自然数に含まれません。
非負整数
0を含む正の整数を「非負整数」と呼びます。非負整数は、0, 1, 2, 3, 4, 5…のように、0を含むすべての正の整数を表します。
整数
整数とは、正の整数、負の整数、そして0を合わせたものです。0以上の整数を言い換える場合、「非負整数」という言葉を使い、0を含めることを明確にするのが一般的です。
正の整数
0を含まない正の整数を「正の整数」と呼びます。正の整数は、1, 2, 3, 4, 5…のように、0より大きい整数を表します。
全数
「全数」は、自然数に0を加えたものです。0を含む正の整数を表すために使われます。全数は、0, 1, 2, 3, 4, 5…のように、0と正の整数を含むすべての整数を表します。
0は数学的に何ですか?

0 は数学的に何ですか?
数学において、0 は非常に重要な概念であり、多くの分野で重要な役割を果たします。 0 は、数を表す際に欠かせない存在であり、さまざまな数学的演算において重要な役割を果たします。
0 の性質
- 0 は加算の単位元です。 つまり、任意の整数 n に対して、n + 0 = n が成り立ちます。
- 0 は乗算の零元です。 つまり、任意の整数 n に対して、n × 0 = 0 が成り立ちます。
- 0 は自然数ではありません。 自然数は 1 から始まる数列であり、0 は含まれません。
- 0 は整数です。 整数は、正の整数、負の整数、および 0 を含む数です。
- 0 は有理数です。 有理数は、整数 p と整数 q (q ≠ 0) を用いて p/q と表すことができる数です。0 は 0/1 と表せるため、有理数です。
0 の歴史
0 は、紀元前 3 世紀のバビロニア文明で初めて使用されました。その後、インド文明やイスラム文明で発展し、現代の数学で広く使用されるようになりました。 0 の概念は、数の体系を理解する上で非常に重要であり、数学の発展に大きな影響を与えました。
0 の応用
- 位置記数法: 0 は、位取り記数法において重要な役割を果たします。例えば、100 は、1 × 102 + 0 × 101 + 0 × 100 と表すことができ、0 はそれぞれの桁の値を決定する上で重要です。
- 方程式: 0 は、方程式の解を求める際に重要な役割を果たします。例えば、x + 3 = 0 の解は x = -3 です。0 は、方程式の解がゼロであることを示します。
- コンピュータ科学: 0 は、コンピュータ科学において、ビットを表現する際に使用されます。0 は “オフ” を表し、1 は “オン” を表します。コンピュータは、0 と 1 の組み合わせによって情報を処理します。
0 の哲学
0 は、数学的な概念を超えて、哲学的な意味合いも持ちます。0 は、無、空虚、何もない状態を表すことができます。 0 は、存在と非存在の境界であり、無限の可能性を秘めているとも言えます。
整数には0は含まれますか?
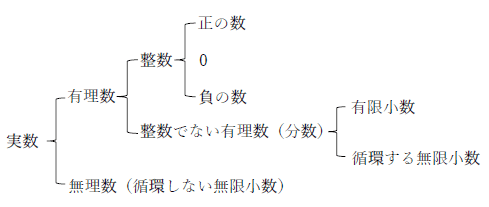
はい、整数には0が含まれます。整数とは、正の整数、負の整数、そして0を含む数の集合です。
整数の定義
整数の定義は、数学の分野によって異なる場合があります。しかし、一般的には、整数は正の整数、負の整数、そして0を含む数の集合として定義されます。
整数の種類
整数は、その性質によっていくつかの種類に分類されます。
- 自然数: 1, 2, 3, 4, …などの正の整数です。
- 正の整数: 1, 2, 3, 4, …などの自然数です。
- 負の整数: -1, -2, -3, -4, …などの負の数です。
- ゼロ: 0は、正の整数でも負の整数でもありません。
整数の性質
整数には、いくつかの重要な性質があります。
- 加算、減算、乗算が閉じている: 2つの整数を加算、減算、乗算しても、その結果は常に整数になります。
- 順序付けられている: 整数は、小さい順から大きい順に並べることができます。
- 無限に存在する: 正の整数、負の整数、そして0は、無限に存在します。
整数の例
整数の例として、以下のものが挙げられます。
- 1, 2, 3, 4, 5 (正の整数)
- -1, -2, -3, -4, -5 (負の整数)
- 0 (ゼロ)
詳しくは
{0は自然数か?数学の深淵に迫る驚きの真実}について、よくある質問
この疑問は、一見単純に見えるかもしれませんが、数学の基礎を深く理解するための重要な手がかりとなります。自然数とは、1、2、3、4…のように、正の整数のことです。{0}が自然数であるかどうかは、{0}の性質に依存します。
{0}が自然数である場合、どのような性質を持っていますか?
{0}が自然数である場合、以下の性質を持ちます。
- 正の整数である。
- 0を含まない。
- 有限である。
- 順序を持つ。つまり、1、2、3…のように、小さい順に並べることができる。
{0}が自然数でない場合、どのような可能性がありますか?
{0}が自然数でない場合、以下の可能性が考えられます。
- 負の数である。
- 分数である。
- 小数である。
- 無限大である。
- 虚数である。
自然数の概念は、数学のどのような分野で重要ですか?
自然数の概念は、数学の様々な分野において重要です。例えば、
- 算術: 自然数の四則演算は、数学の基礎となります。
- 代数: 自然数は、変数や係数として用いられ、方程式や不等式を解くために不可欠です。
- 幾何学: 自然数は、図形の辺や角の数を表すために使用されます。
- 集合論: 自然数は、集合の要素数を表すために使用されます。
自然数の概念は、数学の基礎を理解する上で不可欠であり、様々な分野に影響を与えています。