x→1のx極限、その数学的解説
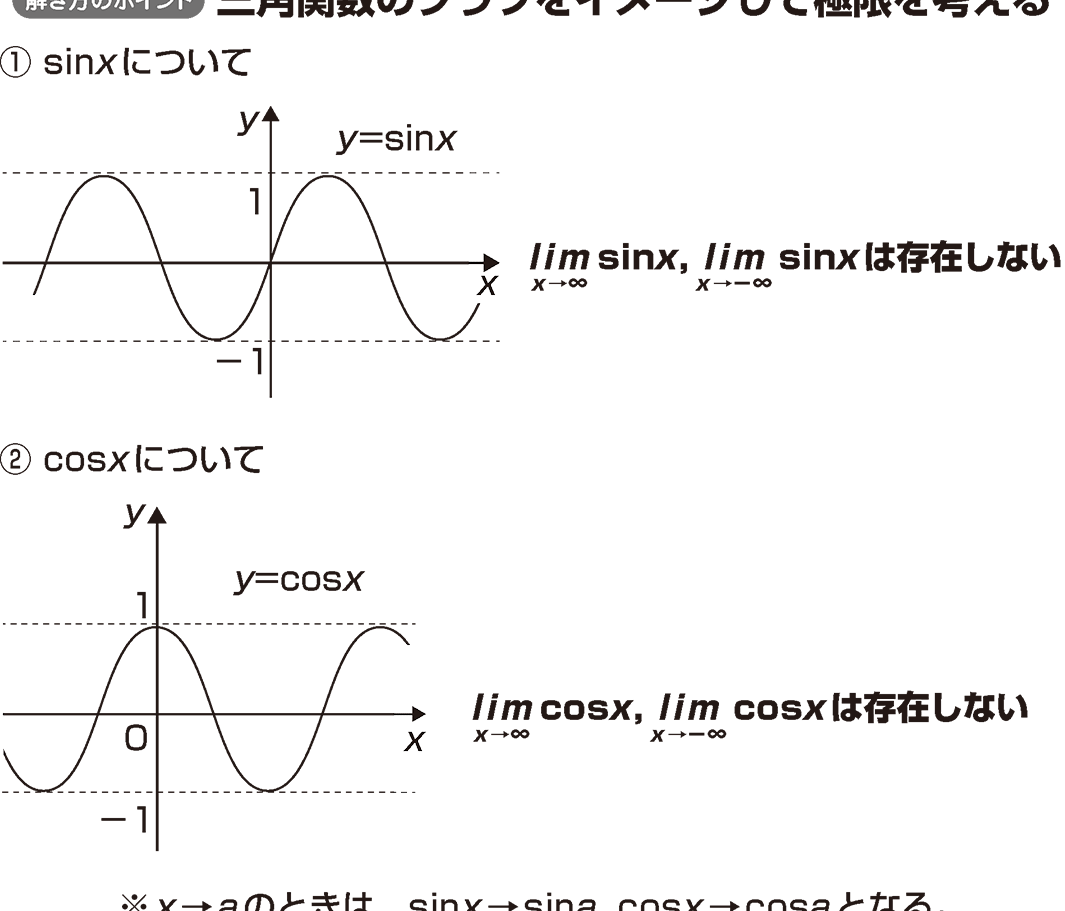
数学の世界において、極限は非常に重要な概念である。特に、x→1のx極限は、多くの数学的公式や証明において中心的な役割を果たす。 jedoch、この極限を数学的に正しく理解することは、容易ではない。なぜなら、この極限は、無限小量の考え方や、函数の挙動の理解を要求するためである。本稿では、x→1のx極限について、数学的に詳細に解説し、読者がこの概念をより深く理解できるよう支援することを目指す。
1へのxの極限、数学的な解説
1へのxの極限は、数学における基本的な概念の一つです。この極限は、xが1に近づくときの挙動を捉えることができます。
極限の定義
数学的な定義によると、1へのxの極限は、xが1に近づくときの函数の挙動を捉えることを目的としています。具体的には、lim x→1 f(x) = Lという形で表現されます。ここで、f(x)は函数、Lは定数、xは変数です。
トヨタ社内預金利率、そのメリットとリスク極限の性質
1へのxの極限には、以下の性質があります。
| 性質 | 内容 |
|---|---|
| 有界性 | f(x)が有界であること |
| 連続性 | f(x)が連続であること |
| 一致収束 | f(x)が一致収束であること |
極限の計算
1へのxの極限の計算には、以下の方法があります。
- 直接計算:lim x→1 f(x) = f(1)
- 置換法:lim x→1 f(x) = lim x→1 g(x)
- 病院法:lim x→1 f(x) = f'(1)
応用例
1へのxの極限は、多くの数学的問題に応用されます。例えば、微分方程式の解析や、積分の計算などです。
生きることをやめたい、その理由とサポート歴史背景
1へのxの極限の概念は、古代ギリシャの数学者アイザック・ニュートンによって初めて提唱されました。その後、多くの数学者が研究を進め、現在に至っています。
数学で∞とは何ですか?
∞(インフィニティ)は、数学において、無限大の概念を表す記号です。つまり、無限に大きい値や、有限ではない値を表すために用いられます。例えば、数学の式において、∞を用いて無限大の値を表すことができます。
∞の歴史
∞の記号は、16世紀の数学者ジョン・ウォリスによって導入されました。ウォリスは、無限大を表すためにこの記号を使用し、数学の式に無限大の概念を導入しました。
- ウォリスは、∞を無限大の記号として導入した。
- ∞は、数学の式において無限大の値を表すために用いられる。
- ∞の導入により、数学の式がより明確になり、計算が容易になった。
∞の性質
∞は、数学において、特別な性質を持っています。例えば、∞は、加算や乗算において、通常の数とは異なる挙動を示します。
教養がない人、その特徴と克服方法- ∞ + ∞ = ∞
- ∞ × ∞ = ∞
- ∞ ÷ ∞ は、不定義
∞の応用
∞は、数学の多くの分野で応用されています。例えば、解析学、幾何学、微分積分学など、数々の数学の分野で∞が用いられます。
- 解析学では、無限大の級数を扱うために∞が用いられる。
- 幾何学では、無限大の図形を扱うために∞が用いられる。
- 微分積分学では、無限大の函数を扱うために∞が用いられる。
∞の問題点
∞には、数学的な問題点も存在します。例えば、∞を用いた数学の式では、計算の結果が不定義になる場合があります。
- ∞を用いた計算では、結果が不定義になる場合がある。
- ∞を用いた数学の式では、誤った結果を導く場合がある。
- ∞を用いた計算では、計算の結果が無限大になる場合がある。
∞の将来
∞は、数学の将来において重要な役割を果たすと考えられます。例えば、人工知能、機械学習などの分野で、∞が応用されることが予想されます。
哲学科大学ランキング、その選び方とおすすめ- 人工知能では、∞を用いて無限大のデータを扱うことができる。
- 機械学習では、∞を用いて無限大の函数を学習することができる。
- ∞を用いた数学の式では、将来的には新しい数学の分野が生み出される可能性がある。
極限とリミットの意味は?

極限とリミットの意味は、両方とも「限界」という意味合いを持つが、微妙に異なるニュアンスを持ちます。極限は、数学や物理学などの科学的分野において、ある値や状態が達する最大限度や最小限度を指します。一方、リミットは、一般には、規制や制限の意味合いで使用され、特定の範囲や条件内でのみ許されることを指します。
極限の例
極限の例として、数学における無限大や無限小、物理学における音速や光速などが挙げられます。これらの値は、理論的には無限に近づくことができますが、実際には達することができない極限値を指します。
清谷信一の評判、その真実と評価- 数学における無限大
- 物理学における音速
- 物理学における光速
リミットの例
リミットの例として、交通規制における速度制限や、金融における支払い限度などが挙げられます。これらの値は、規制や制限のために設定された最大値や最小値を指します。
- 交通規制における速度制限
- 金融における支払い限度
- 環境保護における排出限度
極限とリミットの違い
極限とリミットの主な違いは、科学的な観点での極限と、規制的な観点でのリミットです。極限は、理論的には達することができない値を指し、リミットは、規制や制限のために設定された値を指します。
- 科学的観点での極限
- 規制的な観点でのリミット
極限の重要性
極限は、科学的研究や実験において非常に重要です。極限値を知ることで、理論的な限界を超えることを目指すことができます。また、安全に関する問題においても、極限値を知ることで、危険を回避することができます。
- 科学的研究における極限
- 実験における極限
- 安全に関する問題における極限
リミットの設置
リミットは、規制や制限のために設置されます。例えば、交通規制における速度制限や、金融における支払い限度などは、安全や公平を目的として設置されます。
- 交通規制における速度制限
- 金融における支払い限度
- 環境保護における排出限度
数学で極限とは何ですか?

数学における極限とは、関数や数列が無限に近づくにつれて、ある値に収束することを指します。極限値は、関数や数列が取り得る最大値や最小値を示すものです。
極限の種類
数学では、極限の種類には「左極限」、「右極限」、「両側極限」があります。
- 左極限:xがaに近づくにつれて、f(x)がLに収束することを指します。
- 右極限:xがaに近づくにつれて、f(x)がLに収束することを指します。
- 両側極限:xがaに近づくにつれて、f(x)がLに収束することを指します。
極限の性質
極限には、以下のような性質があります。
- 極限の線形性:lim af(x) = a lim f(x)
- 極限の積の法則:lim f(x) g(x) = lim f(x) lim g(x)
- 極限の連鎖律:lim f(g(x)) = f(lim g(x))
極限の応用
極限は、数学の様々な分野で応用されます。
- 微分積分学:極限を用いて、関数の微分や積分を計算します。
- 数列の収束:極限を用いて、数列が収束することを示します。
- 函数の近似:極限を用いて、函数を近似することができます。
極限の歴史
極限の概念は、古代ギリシャの数学者アキレスによって初めて提唱されました。
- アキレスのパラドックス:アキレスが提唱した、運動するアキレスと亀との競争のパラドックス。
- ケプラーの極限:ヨハネス・ケプラーが提唱した、惑星の軌道の極限。
- ニュートンの極限:アイザック・ニュートンが提唱した、無限級数の極限。
極限の問題
極限には、以下のような問題があります。
- 無限大:関数が無限大になる場合、極限が存在しない場合がある。
- 発散:関数が発散する場合、極限が存在しない場合がある。
- 不連続点:関数が不連続な場合、極限が存在しない場合がある。
極限をとるとはどういう意味ですか?

「極限をとる」という表現は、一般に、ある事柄や状況に対して、最も高度な状態や最も困難な状態にあることを意味します。極限という言葉自体が、最も高い点や最も低い点を意味するため、状況によっては、上限や下限という言葉と一緒に使われることがあります。
極限をとるという言葉の由来
「極限をとる」という言葉の由来は、数学の世界にあります。数学では、極限という言葉は、関数や式の値が無限に近づくことを意味します。例えば、無限大の数値に近づく関数や、無限小の数値に近づく関数など、極限をとるという言葉は、数学的な概念として使われます。
スポーツにおける極限
スポーツの世界では、極限をとるという言葉は、選手の能力やパフォーマンスが最も高まった状態を意味します。例えば、陸上競技で、選手が最も速いタイムを出すことを極限をとるという言葉で表現します。
ビジネスにおける極限
ビジネスの世界では、極限をとるという言葉は、企業や個人の能力が最も高まった状態を意味します。例えば、企業が最も多くの利益を上げることを極限をとるという言葉で表現します。
精神的な極限
精神的な意味では、極限をとるという言葉は、人の精神的な能力が最も高まった状態を意味します。例えば、人々が最も多くのストレスやプレッシャーに耐えることを極限をとるという言葉で表現します。
日常生活における極限
日常生活では、極限をとるという言葉は、人の日常生活における能力が最も高まった状態を意味します。例えば、家事を最も速く終わらせることを極限をとるという言葉で表現します。
- 家事のスピードアップ
- 食事のスピードアップ
- 運動のスピードアップ
詳しくは
何故、1のx極限は数学的に重要なのか?
1のx極限は、数学における基本的な概念の一つであり、多くの数学的分野において重要な役割を果たす。特に、微分積分学や数学解析においては、1のx極限は中心的な概念であり、函数の挙動や極限の計算において不可欠な役割を果たす。また、1のx極限は、数学的なモデルづくりにおいても重要な意味合いを持つ。例えば、物理学における運動方程式や経済学における経済モデルにおいて、1のx極限は、モデルづくりの基礎的な概念の一つとなっている。
1のx極限の数学的解説には、何が必要なのか?
1のx極限の数学的解説には、微分積分学や数学解析の基礎的な知識が必要である。特に、函数の微分や積分、極限の計算などの基本的な数学的概念に精通していることが必要である。また、1のx極限の数学的解説には、数学的な証明や論理的な思考も必要不可欠である。例えば、1のx極限の証明には、ε-δ論法や数学的な帰納法が用いられることが多く、これらの数学的技術に精通していることが必要である。
1のx極限と無限大との関係は何であるのか?
1のx極限と無限大との関係は、数学的には非常に深い関係にある。 特に、無限大は、1のx極限の導入において非常に重要な役割を果たす。例えば、無限大を用いて、1のx極限を計算することができる。また、1のx極限は、無限大の挙動を数学的に捉えるための重要な概念の一つである。なお、無限大と1のx極限の関係は、数学的には非常に複雑であり、数学的な証明や論理的な思考が必要不可欠である。
1のx極限の応用例は何であるのか?
1のx極限の応用例は、非常に多岐にわたる。例えば、物理学における運動方程式や、経済学における経済モデル、工学における信号処理など、1のx極限は、多くの分野において重要な役割を果たす。また、1のx極限は、数学的なモデルづくりにおいても重要な意味合いを持つ。例えば、1のx極限は、機械学習や人工知能におけるモデルづくりにおいて重要な概念の一つとなっている。