Y=1/Xグラフ、その性質と理解のためのポイント
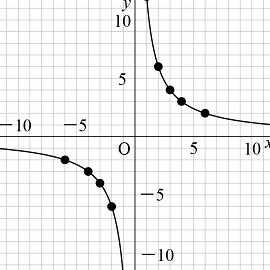
グラフを学ぶ上で、Y=1/Xという特別な形状を持ち、様々な分野で重要な役割を果たすグラフが存在します。このグラフは、数学や物理、生物学などの諸分野において、重要な関係性を表現するために利用されます。このグラフの性質を正しく理解するためには、どのような点に注意すればよいのか、また、このグラフが現れる様々な場面での意義について、理解を深める必要があります。この記事では、Y=1/Xグラフの性質と、理解のためのポイントについて、分かりやすく説明します。
Y=1/Xグラフの理解のための基礎知識
Y=1/Xグラフは、数学や物理学、工学などの分野で頻繁に登場するグラフですが、その性質や特徴を把握することが重要です。このグラフは、逆比例関係を示すもので、X軸とY軸の関係を示しています。
逆比例関係の性質
Y=1/Xグラフは、逆比例関係を示すグラフです。この関係において、X軸の値が大きくなると、Y軸の値は小さくなります。一方、X軸の値が小さくなると、Y軸の値は大きくなります。この逆比例関係は、多くの自然現象や物理現象にあります。
9時オープンスーパー、その便利さと客層| X軸の値 | Y軸の値 |
|---|---|
| 大 | 小 |
| 小 | 大 |
グラフの形状
Y=1/Xグラフの形状は、曲線状です。この曲線は、X軸とY軸の関係を示しています。曲率が小さい部分では、Y軸の値が大きくなります。一方、曲率が大きい部分では、Y軸の値は小さくなります。
グラフの特徴
Y=1/Xグラフには、以下のような特徴があります。対称点があり、X軸とY軸が交差する点では、Y軸の値が1になります。また、グラフの形状は、非線形であるため、予測が困難です。
問題点
Y=1/Xグラフには、以下のような問題点があります。無限大の値が存在するため、計算やグラフの描画に問題が生じます。また、グラフの形状が非線形であるため、予測や解析が困難です。
ホテルのベッドを汚した、その対応と対策応用例
Y=1/Xグラフは、多くの分野で応用されています。物理学では、重力の逆比例関係を示すために使用されます。工学では、信号処理や制御理論に応用されます。経済学では、需要と価格の関係を示すために使用されます。
反比例を考えるポイントは?
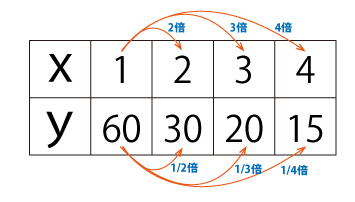
反比例を考えるポイントは、以下の通りです。
反比例の定義と意味
反比例とは、2つの量が逆に変化する関係を指します。逆に変化するということは、片方の量が増加すると、他方の量が減少することを意味します。例えば、価格と需要のように、片方が高まるにつれて他方が減少する関係が反比例です。
反比例の種類
反比例には、以下のような種類があります。
太陽フレアと地震、その関係と科学的解明- 完全反比例:片方の量が0になると、他方の量が無限大になる関係。
- 不完全反比例:片方の量が0にならない場合は、他方の量が有限である関係。
- 部分反比例:片方の量が一定の範囲内で変化すると、他方の量が一定の範囲内で変化する関係。
反比例の例
反比例の例として、以下のようなものがあります。
- 価格と需要:価格が高まるにつれて需要が減少する。
- 速度と時間:速度が速くなるにつれて時間が短縮する。
- 体重と運動能力:体重が減少するにつれて運動能力が向上する。
反比例の計算
反比例の計算には、以下の式を用います。xy=k(kは定数)。この式を用いて、片方の量から他方の量を計算することができます。
反比例の応用
反比例は、様々な分野で応用されます。
「Dreams Come True」で間違うその理由- 経済学:需要と供給の関係や、価格と需要の関係。
- 物理学:速度と時間の関係や、力と距離の関係。
- 生物学:体重と運動能力の関係や、栄養素と生長の関係。
比例と反比例の式を求めるポイントは?

比例と反比例の式を求めるポイントは、以下の通りです。
比例の式とは
比例の式とは、ある数量が他の数量に対して一定の率で変化する関係を示す式のことです。比例係数と呼ばれる定数をかけることで、相互に関連する数量同士の関係を表現することができます。比例の式は、
「何言ってんだ」、その意外な使い方- 数量の比較
- 割合の計算
- 変化の関係
などの問題に応用されます。
反比例の式とは
反比例の式とは、ある数量が他の数量に対して逆の率で変化する関係を示す式のことです。反比例係数と呼ばれる定数をかけることで、相互に関連する数量同士の関係を表現することができます。反比例の式は、
- 数量の逆関係
- 反比例関係
- 数量の相互関係
などの問題に応用されます。
比例と反比例の式の違い
比例の式と反比例の式の最大の違いは、係数の符号です。比例の式では、係数は正の値を取り、反比例の式では、係数は負の値を取ります。また、比例の式では、数量が増加すると他の数量も増加する関係にあるのに対し、反比例の式では、数量が増加すると他の数量は減少する関係にあるという点も異なります。
- 係数の符号
- 数量の関係
- 式の形
比例と反比例の式の応用
比例と反比例の式は、科学、工学、経済など、幅広い分野で応用されます。例えば、
- 物理学における運動の関係
- 化学における反応の関係
- 経済学における需要と供給の関係
など、多くの問題に比例や反比例の関係が見られます。
比例と反比例の式の計算
比例と反比例の式の計算には、式の展開や係数の計算が必要です。まず、式を展開し、係数を計算し、最後に式を整理することで、比例や反比例の関係を明らかにすることができます。
- 式の展開
- 係数の計算
- 式の整理
Yはxに反比例するはどういうことか?
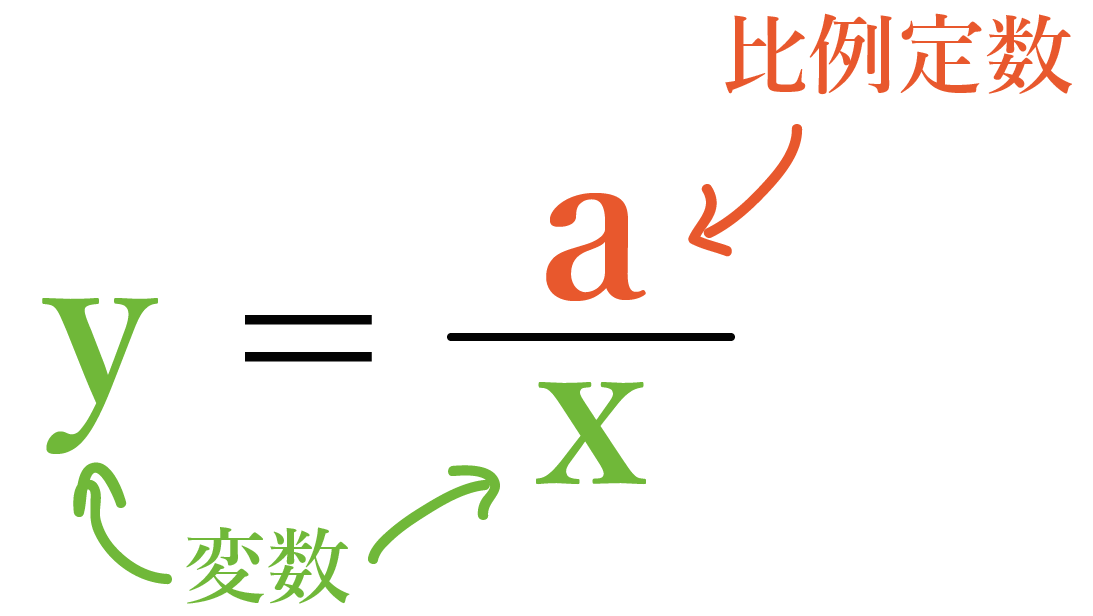
Yはxに反比例するというのは、Yの値がxの値に反比例する関係にあるということを意味します。反比例関係とは、xの値が増加するにつれてYの値が減少する関係、或いはxの値が減少するにつれてYの値が増加する関係を指します。
反比例関係の性質
反比例関係には、以下の性質があります。
- Yの値がxの値に反比例するため、xの値が0になった場合、Yの値は無限大になります。
- xの値が増加するにつれてYの値は減少します。
- xの値が減少するにつれてYの値は増加します。
反比例関係の例
反比例関係の例として、以下のような場合があります。
- 時間と距離の関係:ある地点までの距離が増加するにつれて、到達するまでの時間は減少します。
- 重さと体積の関係:ある物体の重さが増加するにつれて、体積は減少します。
- 圧力と体積の関係:気体の圧力が増加するにつれて、体積は減少します。
反比例関係のグラフ
反比例関係のグラフは、xy座標上に描かれます。x軸にはxの値、y軸にはYの値が取り扱われます。曲線は、開 反比例関係の場合には、x軸とy軸のどちらかが増加するにつれて、もう一方が減少します。
反比例関係の公式
反比例関係の公式は、Y = k/x という形で表されます。ここで、k は比例係数です。比例係数は、xの値が変わるとYの値がどのように変わるかを示す係数です。
反比例関係の応用
反比例関係には、以下のような応用があります。
- 科学:反比例関係は、物理学、化学、生物学などの分野で観察される関係です。
- 工学:反比例関係は、機械工学、電気工学、電子工学などの分野で応用されます。
- 経済:反比例関係は、経済学において、需要と供給の関係や、価格と数量の関係などで観察されます。
一次関数で大切なことは何ですか?

一次関数は、数学における基本的な概念の一つです。一次関数は、独立変数の値によって従属変数の値が一意に定まり、グラフが一直線になる関数です。一次関数は、直線の式として表現され、一般的にはy=ax+bの形で表されます。
一次関数の特徴
一次関数の特徴として、以下のような点が挙げられます。
- 直線のグラフ:一次関数のグラフは一直線になる。
- 単調増加:一次関数は、独立変数の値が増加すると従属変数の値も増加する。
- 反比例:一次関数は、独立変数の値が減少すると従属変数の値も減少する。
一次関数の応用
一次関数は、実生活において様々な場面で応用されます。
- 経済学:一次関数は、需要関数や供給関数のグラフを表すために用いられる。
- 物理学:一次関数は、運動の距離や速度を表すために用いられる。
- 工学:一次関数は、機械の運動や電気回路の解析に用いられる。
一次関数の式の変形
一次関数の式は、以下のような形に変形することができます。
- 点斜式:y-y1=a(x-x1)
- 斜辺式:y=ax+b
- 交点式:x/a+y/b=1
一次関数のグラフの描き方
一次関数のグラフを描くためには、以下のような手順を踏みます。
- 式の設定:一次関数の式を設定する。
- 座標軸の設定:x軸とy軸を設定する。
- 点のプロット:式に基づいて、点をプロットする。
一次関数の問題の解き方
一次関数の問題を解くためには、以下のような手順を踏みます。
- 式の設定:一次関数の式を設定する。
- 式の変形:式を変形して、目的の式に変換する。
- 解の計算:式に基づいて、解を計算する。
詳しくは
Q1: 何故Y=1/Xグラフは反比例関係を示すのか?
Y=1/Xグラフは、反比例関係を示すグラフです。このグラフは、X軸とY軸の間に逆さまの関係があることを示しています。つまり、Xの値が大きくなると、Yの値は小さくなり、Xの値が小さくなると、Yの値は大きくなります。この関係は、比例関係とは逆の関係であり、実際には、多くの自然現象や社会現象で観察される関係です。
Q2: Y=1/Xグラフの性質は何ですか?
Y=1/Xグラフの性質として、以下のような特徴があります。まず、曲線はgetAsymptoteに近づくという特徴があります。また、曲線は対称であり、X軸とY軸が交わる点を中心として、左右対称に分布しています。また、曲線の形状は、Xの値によって変化し、Xの値が大きくなると、曲線は水平方向に伸び、Xの値が小さくなると、曲線は垂直方向に伸びます。
Q3: Y=1/Xグラフを理解するために必要なポイントは何ですか?
Y=1/Xグラフを理解するために必要なポイントとして、以下のような点が挙げられます。まず、グラフの読み方を理解することが重要です。Y=1/Xグラフは、X軸とY軸の間に逆さまの関係があるため、グラフを読むときには、Xの値を基準にして、Yの値を読み取る必要があります。また、グラフの形状を理解することが重要です。曲線の形状は、Xの値によって変化するため、グラフの形状を理解することで、関係の変化を把握することができます。
Q4: Y=1/Xグラフを実際にどのように活用することができますか?
Y=1/Xグラフを実際に活用する方法として、以下のような例が挙げられます。まず、科学的研究において、Y=1/Xグラフは、実験結果の分析や、理論の検証に用いることができます。また、経済的分析において、Y=1/Xグラフは、需要と供給の関係を分析するために用いることができます。また、工程学において、Y=1/Xグラフは、システムの最適化や、性能の評価に用いることができます。






